Two tanks | Theory of Hybrid Systems

Classification

# of variables	# of modes	# of jumps
2	4	7

Type	Continuous dynamics	Guards & Invariants	Resets
hybrid	linear polynomial	hyperplane & half-space	identity

Download

Flow*	flow*_files
SpaceEx	spaceEx_files

Model description

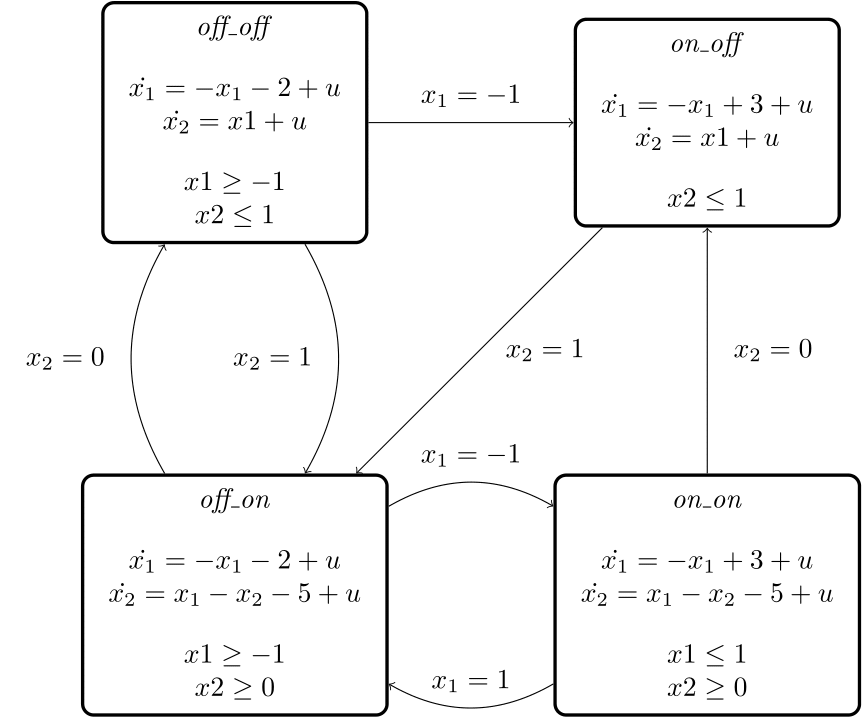
The considered benchmark presented in Fig.1(a) consists of two tanks. The liquid in the first tank comes from two outside sources: a constant inflow source and a second source equipped with a controlled valve valve1, with flows $Q_0$ and $Q_1$ respectively. A drain placed at the bottom of tank 1 allows the liquid to flow into tank 2 with flow $Q_A$ .

Tank 2 is itself equipped with two drains. In the first one a pump is placed to assure a constant liquid outflow $Q_B$ whereas the flow in the second one $Q_2$ is controlled by an electro-valve valve2.Both valves can take the states On/Off. This results consequently in four possible discrete modes for the hybrid automaton. The liquid levels in tank i is given by $x_i$ .

The dynamics of the above system is defined by the following differential equations:

$\dot{x}_1 = \left\{ \begin{array}{l l} -x_1-2 + [-0.1,0.1] & \quad \text{if $valve_1$ is Off}\\ -x_1+3 + [-0.1,0.1] & \quad \text{if $valve_1$ is On} \end{array} \right. \] \[\dot{x}_2 = \left\{ \begin{array}{l l} x_1+ [-0.1,0.1] & \quad \text{if $valve_2$ is Off}\\ x_1-x_2-5+ [-0.1,0.1] & \quad \text{if $valve_2$ is On} \end{array} \right.$

Reachability settings

We consider an initial set of

$x_1 \in [1.5,2.5]$
$x_2 = 1$

and the starting location $off\_off$ , a time horizon $T=5s$ , and a time step $r=0.1s$ . The set of bad states are all states, where $x_2 <= -0.7$ .

Results

Fig.2 shows the flowpipes computed for the above-mentioned parameters using a) HyReach and b) SpaceEx. The results given in Fig. 2 show tightness difference between the two obtained flowpipes, although both proposed tools are based on the same reachability analysis technique using support functions.

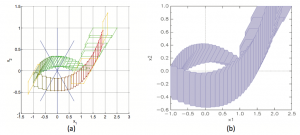
Figure 2: Flowpipe of the two-tank system

References

[1] J. Lygeros. Lecture notes on hybrid systems. Technical Report, 2004.

[2] I. A. Hiskens. Stability of limit cycles in hybrid systems. In Proceedings of the 34th Hawaii International Conference on System Sciences (HICSS’01), pages 163-328, IEEE, 2001.

[3] A. Girard. Reachability of Uncertain Linear Systems Using Zonotopes. In Proceedings of the 8th International Workshop on Hybrid Systems: Computation and Control (HSCC’05), Volume 3414 of LNCS, pp 291-305, Springer, 2005.