Classification
| type | # of discrete variables | # of clocks | # of rest variables | # of controller modes | # of plant modes | # of jumps |
|---|---|---|---|---|---|---|
| original | 0 | 0 | 8 | 6 | 2 | 18 |
| timed | 0 | 1 | 7 | 6 | 2 | 18 |
| discrete | 5 | 0 | 3 | 6 | 2 | 18 |
| timed & discrete | 5 | 1 | 7 | 6 | 2 | 18 |
| Type | Continuous dynamics | Guards & Invariants | Resets |
|---|---|---|---|
| hybrid | linear polynomial | hyperplane & half-space | constant |
Download
| SpaceEx | spaceEx_files |
| HyPro | hypro_files |
Model description
In this benchmark a heater with a thermostat controller is modelled. Initially, the temperature is ![]() and the heater is on. The controller keeps the temperature between
and the heater is on. The controller keeps the temperature between ![]() and
and ![]() . The heater is switched off if the temperature rises above
. The heater is switched off if the temperature rises above ![]() and it is switched on at a
and it is switched on at a
temperature below ![]() . Adding a controller to the model introduces new variables for the low and high temperature sensors in the controller, a variable for the actuator (heater) state in the plant and the controller, and a variable to store the controller mode. Additionally, we introduce a new clock for the cycle time of the PLC. The global time horizon is 10 seconds and the PLC cycle time is 0.5 seconds.
. Adding a controller to the model introduces new variables for the low and high temperature sensors in the controller, a variable for the actuator (heater) state in the plant and the controller, and a variable to store the controller mode. Additionally, we introduce a new clock for the cycle time of the PLC. The global time horizon is 10 seconds and the PLC cycle time is 0.5 seconds.
The dynamics of the temperature is defined by the following differential equations:
![]()
Reachability settings
We consider an initial set of
and the starting location ![]() , a time horizon
, a time horizon ![]() , a PLC cycle duration of
, a PLC cycle duration of ![]() , and a time step
, and a time step ![]() .
.
Results
Fig.1 shows the flowpipes computed for the above-mentioned parameters using a) Hypro and b) SpaceEx.
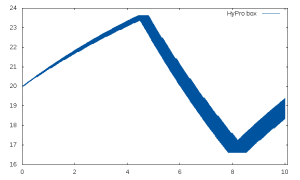
Figure 1: Flowpipe of the thermostat system with controller
References
[1] J. Nellen. Analysis and synthesis of hybrid systems in engineering applications. PhD Thesis, RWTH Aachen University, 2016.
[2] S. Schupp et al.. Divide and conquer: Variable set separation in hybrid systems reachability analysis. Submitted to (QAPL’17).