Steam Governor | Theory of Hybrid Systems

Download

Flow*

Model description

We study the steam governor system described in [1]. It is a continuous system defined by the following ODE.

$\left\{ \begin{array}{lcl} \dot{x} & = & y \\ \dot{y} & = & z^2 \cdot \sin(x) \cdot \cos(x) - \sin(x) - \epsilon\cdot y \\ \dot{z} & = & \alpha \cdot (\cos(x) - \beta) \end{array} \right.$

wherein $\epsilon$ , $\alpha$ and $\beta$ are constants. As it is proved in [1] that the system has an asymptotically stable equilibrium when $\epsilon > 2\cdot \alpha \cdot \beta^{\frac{3}{2}}$ .

Reachability settings

We consider the initial set $x\in [0.9,1.1]$ , $y\in [-0.1,0.1]$ , $z \in [0.9,1.1]$ and the constants $\epsilon = 3$ , $\alpha = 1$ and $\beta = 1$ .

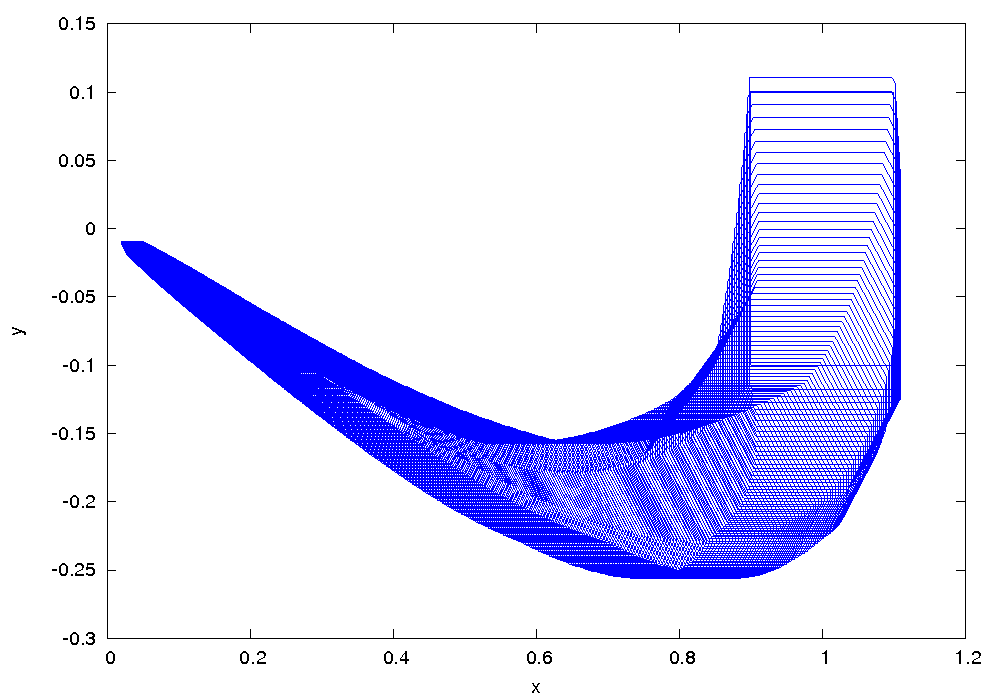
Results

The following figure shows an overapproximation computed by Flow* for the time horizon $[0,10]$ :

References

[1] J. Sotomayor, L. Mello, D. Braga. Bifurcation analysis of the Watt governor system. Computational & Applied Mathematics, Vol. 26, No. 1, pages 19-44, SBMAC, 2007.