Classification
| # of variables | # of modes | # of jumps |
|---|---|---|
| 2 | 1 | 1 |
| Type | Continuous dynamics | Guards & Invariants | Resets |
|---|---|---|---|
| hybrid | linear polynomial | linear polynomial | linear polynomial |
Download
| Flow* model I | neuron_I.model |
| Flow* model II | neuron_II.model |
Description of model I
The general dynamics of the model of spiking neurons is defined by the following ODE.
![]()
wherein the constant parameters are given by ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() . The value of
. The value of ![]() is
is ![]() when
when ![]() , otherwise it is
, otherwise it is ![]() . Whenever the value of
. Whenever the value of ![]() reaches
reaches ![]() , its value is reset to
, its value is reset to ![]() and meanwhile
and meanwhile ![]() is updated to
is updated to ![]() .
.
Reachability settings for model I
We consider the initial set defined by ![]() ,
, ![]() .
.
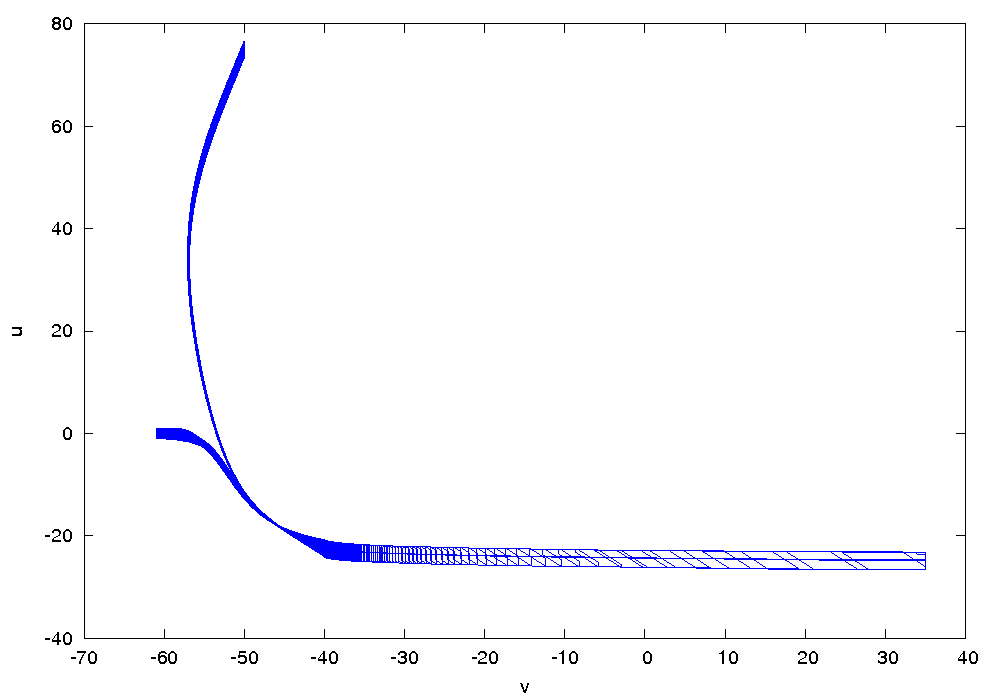
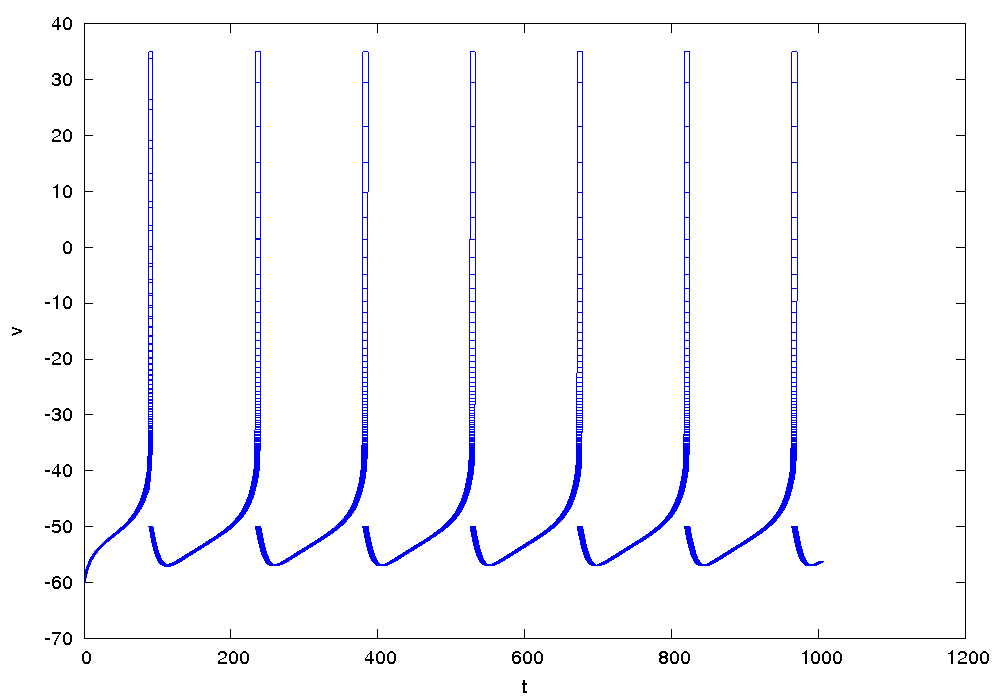
Results for model I
The following figures show an overapproximation computed by Flow* for the time horizon ![]() .
.
Description of model II
As the second example, the constant parameters are given by ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() . The values of
. The values of ![]() ,
, ![]() are reset to
are reset to ![]() and
and ![]() respectively when
respectively when ![]() .
.
Reachability settings for model II
We consider the initial set defined by ![]() ,
, ![]() .
.
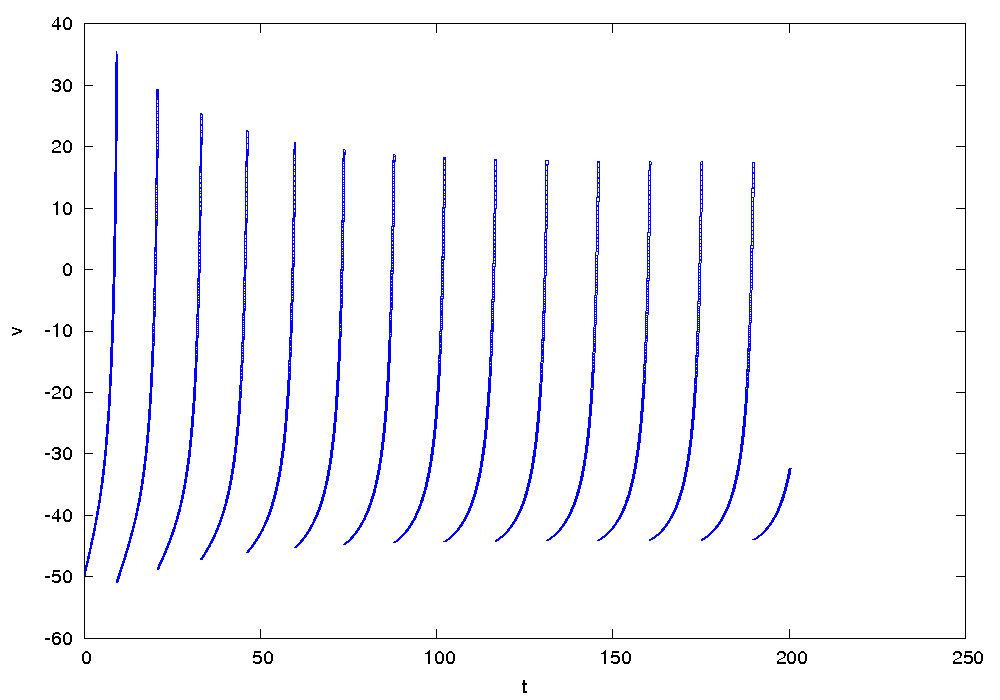
Results for model II
The following figures show an overapproximation computed by Flow* for the time horizon ![]() .
.