Model description
The general dynamics of the model of spiking neurons is defined by the following ODE.
![]()
wherein the constant parameters are given by ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() . The values of
. The values of ![]() ,
, ![]() are reset to
are reset to ![]() and
and ![]() respectively when
respectively when ![]() .
.
Reachability setting
We consider the initial set defined by ![]() ,
, ![]() .
.
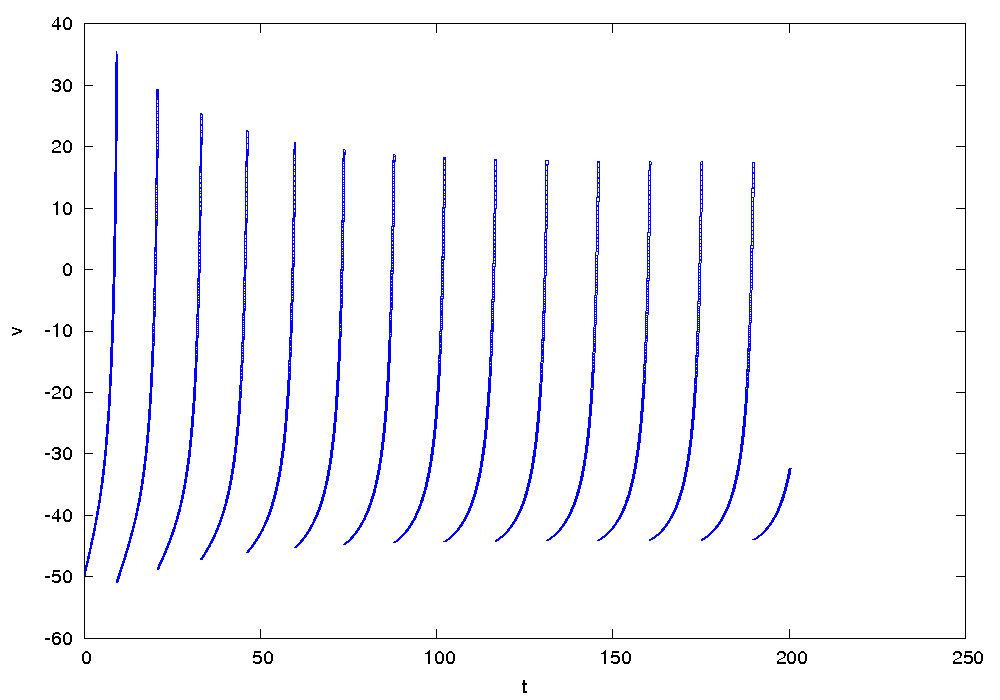
Result
The following figures show an overapproximation computed by Flow* for the time horizon ![]() .
.