H2-based N-vehicle platoon | Theory of Hybrid Systems

Download

Flow*	vehicle_platoon_5 vehicle_platoon_10
SpaceEx	5_vehicles, 10_vehicles

Model description

The proposed benchmark consists of $n$ autonomously-driven vehicles. These vehicles follow longitudinally a leader located at the head of the formation. The collaboration process is realized by networking the vehicles inside the platoon via a communication network. In this example, the vehicles exchange information about their relative positions, their relative velocities as well as their actual accelarations measured with on-board sensors via a wireless communication network.

Fig.1: The relative position between vehicles inside the platoon.

The relative position $e_i$ of vehicle $i$ is defined as the difference between the distance $d_i$ to its predecessor and a reference distance $d_{ref,i}$ (see fig.1).

(1) $\begin{equation*}e_i = d_i -d_{ref,i}.\end{equation*}$

The relative velocity of vehicle $i$ is the derivative of its relative position $\dot{e_i}$ and the accelaration is defined as $a_i$ .

Each vehicle $i$ inside the platoon will be then described by the state vector $x_i = [e_i, \dot{e_i}, a_i]$ . In case of a five vehicle longitudinal formation, the state vector takes this form $x = [e_1, \dot{e_1}, a_1, e_2, \dot{e_2}, a_2, e_3, \dot{e_3}, a_3, e_4, \dot{e_4}, a_4, e_5, \dot{e_5}, a_5]$ .

The control design aims firstly at stabilizing the controlled platoon while assuring minimum relative distances and secondly at guaranteeing a quick response to disturbances but with bounded oscillations and overshoots. The main goal thereby is to avoid collisions inside the platoon. These objectives can be expressed as a norm 2 (H2) optimization problem. Details can be found in [1,2,3].

In addition, a particular control design objective related to the nature of this application, the so-called string stability, must be also taken in consideration. The string stability assures the attenuation of the relative distance while moving from the head of the platoon to its bottom. This is generally formulated as a norm infinity (H infinity) optimization problem [1,2,3].

For the sake of simplicity, the control design considered here does not take account of the previous condition. However, this last will be verified using reachability analysis after computing the closed loop system obtained by solving just the H2 optimization problem.

In addition to the previous goal, reachability analysis will be particularly used to determine a lower bound for $d_{ref,i}$ which guarantees a collision-free drinving.

We suppose, in this case that there is communication between all the vehicles so that relevant information for control is always available. The controlled platoon can be then modeled as a hybrid automaton with a unique location. The invariant is the whole state space and the flow is given by the dynamics of the closed loop system described by the following linear differential equation

(2) $\begin{equation*}\dot x = Ax + Ba_L,\end{equation*}$

where $A$ is a constant system matrix, $B$ is a constant input matrix and $a_L$ the acceleration of the leader considered here as an uncertain input [1,2].

The matrices resulting from the solution of the control problem for $5$ and $10$ vehicles can be obtained as csv files 5_vehicle_dynamic and 10_vehicle_dynamic.

Reachability settings

Setting in the model files

All variables are initially set to be in the interval $[0.9;1.1]$ . The stepsize is set to $0.1$ and the time horizon $T=20$ . The set of bad states are the states, where $x1 \in [-0.5,-0.2]$ .

Additional possible settings

The computation can start with the origin $0_{\mathbb{R}^{15}}$ or with a neighborhood of the origin. The maximum allowed uncertain input set is $[-9,1]m s^{-2}$ .

We aim first to verify if under such a large uncertainty in the input the string stability is hold or not. That means if:

(3) $\begin{align*}e_1> e_2> e_3> e_4> e_5.\end{align*}$

We are then interested in finding the shortest gaps ${e_1}_{min}$ , ${e_2}_{min}$ , ${e_3}_{min}$ , ${e_4}_{min}$ , ${e_5}_{min}$ within the platoon which correspond to the lower bounds of the reachable set in the corresponding directions of the canonical basis.

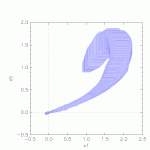
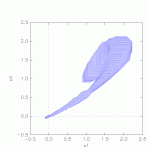
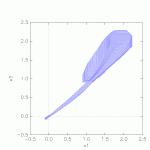
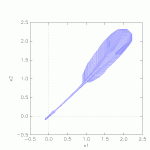
Results

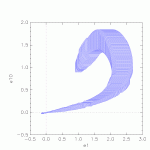
Results of the 5 vehicle platoon gained from SpaceEx:

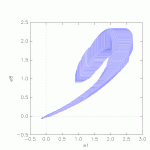
Results of the 10 vehicle platoon gained from SpaceEx:

References

[1] J.P. Maschuw, Platoon Control and Reconfiguration Based on Linear Matrix Inequalities, In: Fortschritt-Berichte VDI, Reihe 8, Mess-, Steuerungs- und Regelungstechnik, volume 1216, ISBN 978-3-18-521608-4, 2012.

[2] J. Maschuw and D. Abel, Longitudinal vehicle guidance in networks with changing communication topology. In AAC 2010, IFAC-Symposium Advances in Automotive Control, München, 2010.

[3] J. Maschuw, and G. Keler, and D. Abel, LMI based control of vehicle platoons for robust longitudinal guidance. In IFAC World Congress, Seoul, 2008.