Lotka-Volterra | Theory of Hybrid Systems

Download

Flow*

Model description

The 2-dimensional Lotka-Volterra system depicts the populations change of a class of predators and a class of preys. The growth rate of preys’ population $x$ over time is given by $\dot{x} = x\cdot (\alpha - \beta \cdot y)$ wherein $\alpha, \beta$ are constant parameters and $y$ is the population of predators. It gives that the number of preys grows exponentially without predation. The population growth of predators is governed by the differential equation $\dot{y} = -y\cdot (\gamma - \delta\cdot x)$ wherein $\gamma, \delta$ are constant parameters. We set those parameters as $\alpha = 1.5$ , $\beta = 1$ , $\gamma = 3$ and $\delta = 1$ .

Reachability setting

We consider the initial set $x\in [4.8,5.2], y \in [1.8,2.2]$ .

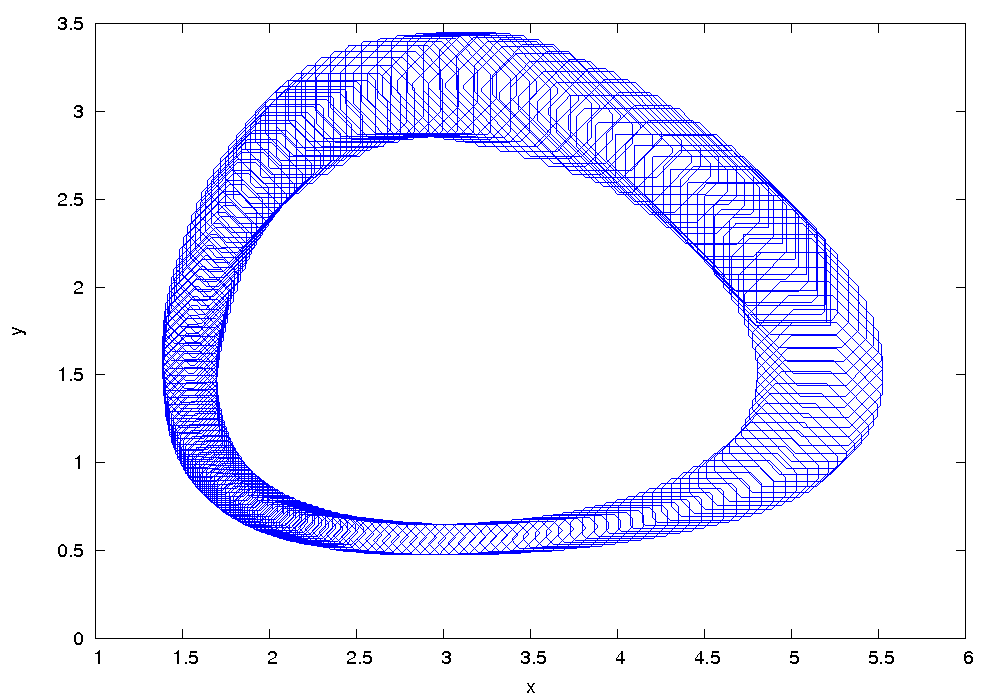
Results

The following figure shows an overapproximation computed by Flow* for the time horizon $[0,5]$ :