Classification
| type | # of discrete variables | # of clocks | # of rest variables | # of controller modes | # of plant modes | # of jumps |
|---|---|---|---|---|---|---|
| original | 0 | 0 | 12 | 8 | 3 | 34 |
| timed | 0 | 1 | 11 | 8 | 3 | 34 |
| discrete | 9 | 0 | 3 | 8 | 3 | 34 |
| timed & discrete | 9 | 1 | 2 | 8 | 3 | 34 |
| Type | Continuous dynamics | Guards & Invariants | Resets |
|---|---|---|---|
| hybrid | constant | hyperplane & half-space | constant |
Download
| SpaceEx | spaceEx_files |
| HyPro | hypro_files |
Model description
This benchmark models a water tank which leaks, i.e., it has a constant outflow. The tank can be refilled from an unlimited external resource with a constant inflow that is larger than the outflow. The PLC controller triggers refilling (by switching a pump on) if a sensor indicates a low water level (![]() ). If the water level is high (
). If the water level is high (![]() ) the controller stops refilling (switches the pump off). Adding the controller introduces two controller input variables for low and high water levels, variables for the actuator (pump) state in the plant and the controller, and a variable to store the controller mode. Furthermore, a new clock is added to model the PLC cycle time. Besides the controller we also model a user which can manually switch
) the controller stops refilling (switches the pump off). Adding the controller introduces two controller input variables for low and high water levels, variables for the actuator (pump) state in the plant and the controller, and a variable to store the controller mode. Furthermore, a new clock is added to model the PLC cycle time. Besides the controller we also model a user which can manually switch
the pump on and off as far as the water level allows it. In our implementation, the user constantly toggles between the pump states on and off. We analyse the system behaviour over a global time horizon of $40$ seconds using a PLC cycle time of $2$ seconds.
The dynamics of the waterlevel of the tank is defined by the following differential equations:
![Rendered by QuickLaTeX.com \[\dot{h} = \left\{ \begin{array}{l l} $\phantom{-}2$ & \quad \text{if the pump is on and the tank is not full}\\ $\phantom{-}2$ & \quad \text{if the tank is full}\\ $-1.5$ & \quad \text{if the pump is off}\\ \end{array} \right. \]](https://ths.rwth-aachen.de/wp-content/ql-cache/quicklatex.com-1ea907cb98e4537fc4802fd78c6ed5d0_l3.png)
Reachability settings
We consider an initial set of
and the starting location ![]() , a time horizon
, a time horizon ![]() , a PLC cycle duration of
, a PLC cycle duration of ![]() , and a time step
, and a time step ![]() .
.
Results
Fig.1 shows the flowpipes computed for the above-mentioned parameters using HyPro.
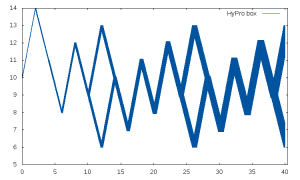
Figure 1: Flowpipe of the leaking tank system with controller
References
[1] J. Nellen. Analysis and synthesis of hybrid systems in engineering applications. PhD Thesis, RWTH Aachen University, 2016.
[2] S. Schupp et al.. Divide and conquer: Variable set separation in hybrid systems reachability analysis. Submitted to (QAPL’17).