Glycemic control (polynomial version) | Theory of Hybrid Systems

Classification

# of variables	# of modes	# of jumps
4	6,9	10,18

Type	Continuous dynamics	Guards & Invariants	Resets
hybrid	non-linear polynomial	linear polynomial	identity

Download

Flow* Strategy I	diabetic_1.model
Flow* Strategy II	diabetic_2.model

Model description

We consider a model of the glycemic control in diabetic patients such that all dynamics are defined by polynomials. The modeling ODE is given by

$\left\{ \begin{array}{lcl} \dot{G} & = & -p_1 \cdot G - X\cdot(G + G_B) + g(t) \\ \dot{X} & = & -p_2\cdot X + p_3\cdot I \\ \dot{I} & = & -n\cdot (I + I_B) + \frac{1}{V_I}\cdot i(t) \end{array} \right.$

such that $G$ is plasma glucose concentration above the basal value $G_B$ and $I$ is the plasma insulin concentration above the basal value $I_B$ . $X$ is the insulin concentration in an interstitial chamber. The constant parameters are given by $p_1 = 0.01$ , $p_2 = 0.025$ , $p_3 = 0.000013$ , $V_I = 12$ , $n = 0.093$ , $G_B = 4.5$ , $I_b = 15$ .

The influx of glucose $g(t)$ after a meal is modeled as

$g(t) = \left\{ \begin{array}{ll} \frac{t}{60} & t \leq 30 \\ \frac{120-t}{180} & t\in (30,120] \\ 0 & t > 120 \end{array}\right.$

while the insulin control strategies $i(t)$ due to [1] and [2] are given by

$i_1(t) = \left\{ \begin{array}{ll} \frac{25}{3} & G(t) \leq 4 \\ \frac{25}{3} (G(t) -3) & G(t) \in (4,8] \\ \frac{125}{3} & G(t) > 8 \end{array} \right.\] \[ i_2(t) = \left \{ \begin{array}{ll} 1 + \frac{2G(t)}{9} & G(t) < 6 \\ \frac{50}{3} & G(t) > 6 \end{array}\right.$

respectively.

Reachability settings

We consider the initial condition $G(0) \in [-2,2]$ , $X(0) = 0$ , $I(0) \in [-0.1,0.1]$ , and the time horizon is given by $[0,360]$ .

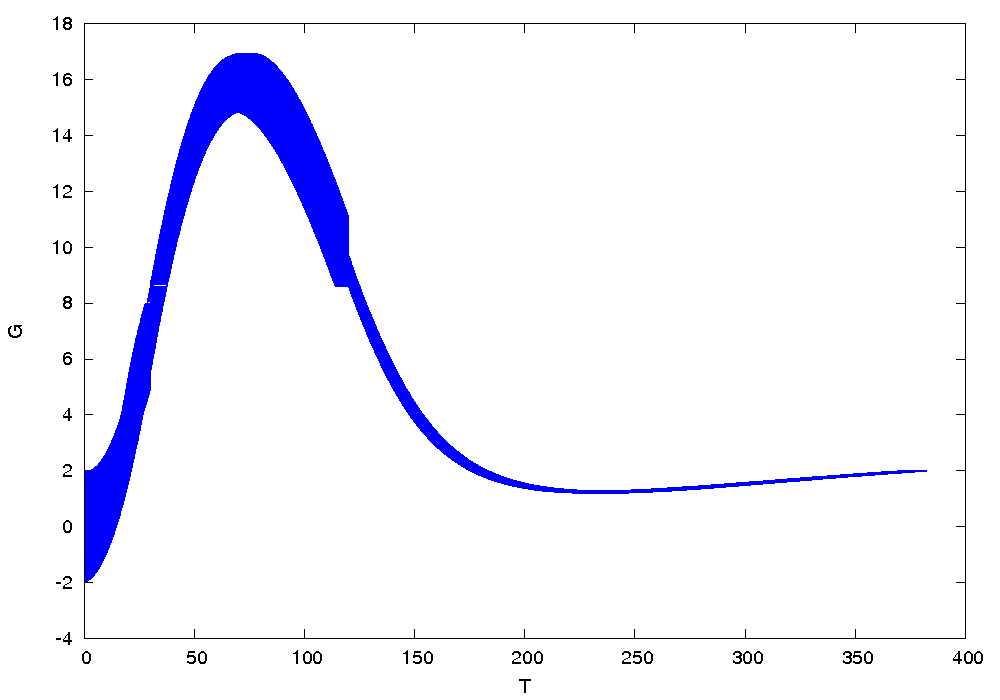
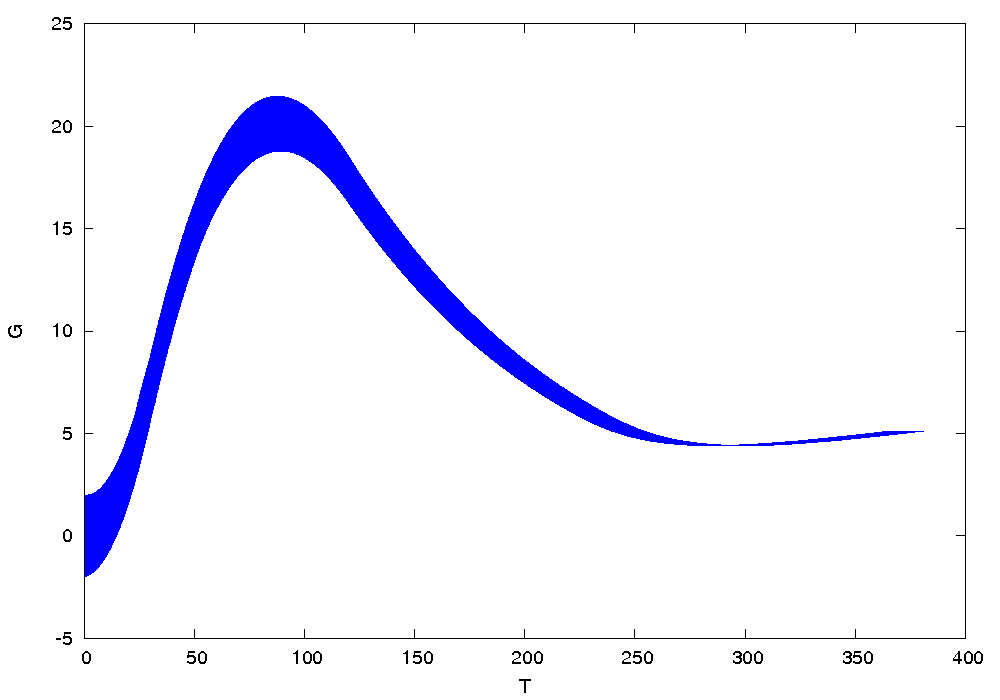
Results

The following figures show an over-approximation computed by Flow* for the first and the second strategies:

References

[1] S. Furler, E. Kraegen, R. Smallwood, D. Chisholm. Blood glucose control by intermittent loop closure in the basal mode: computer simulation studies with a diabetic model. In Diabetes Care, Volume 8, pages 553–561, American Diabetes Association, HighWire Press, 1985.

[2] M. Fisher. A semiclosed-loop algorithm for the control of blood glucose levels in diabetics. In IEEE transactions on biomedical engineering, Volume 38(1), pages 57-61, IEEE,
1991.