Classification
| # of variables | # of modes | # of jumps |
|---|---|---|
| 6-34 | 4 | 4 |
| Type | Continuous dynamics | Guards & Invariants | Resets |
|---|---|---|---|
| hybrid | linear polynomial | hyperplane & half-space | identity |
Download
| Flow* | filtered_oscillator_4, filtered_oscillator_8, filtered_oscillator_16, filtered_oscillator_32 |
| SpaceEx | filtered_oscillator_4, filtered_oscillator_8, filtered_oscillator_16, filtered_oscillator_32 |
Model description
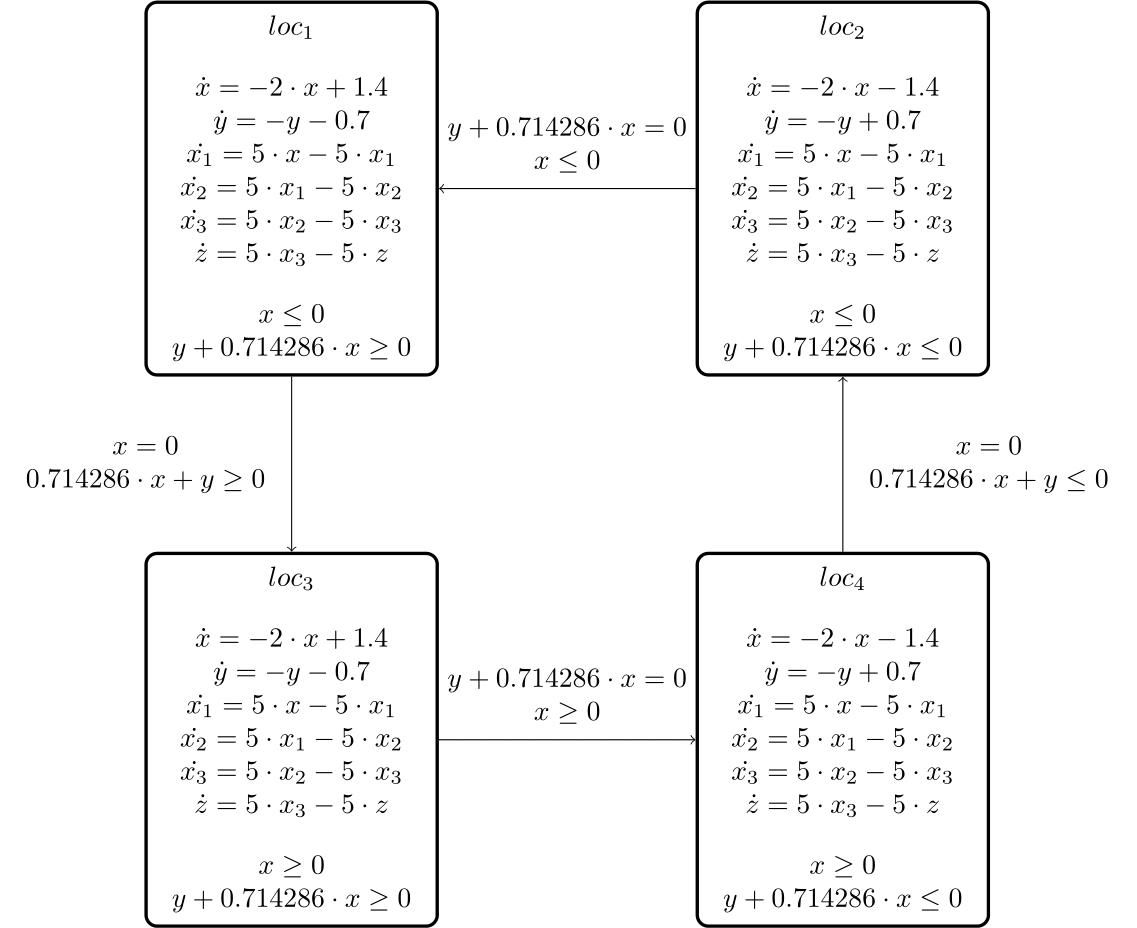
This benchmark consists of a two-dimensional switched oscillator (variables ![]() ) plus an 4-th order filter with state variables
) plus an 4-th order filter with state variables ![]() , and
, and ![]() . The filter smoothens the signal
. The filter smoothens the signal ![]() and has
and has ![]() as the output signal. At the switching planes (diagonal and horizontal in the
as the output signal. At the switching planes (diagonal and horizontal in the ![]() /
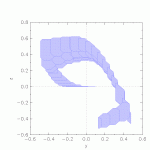
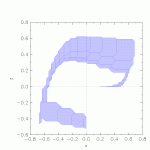
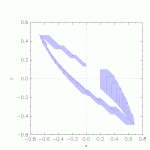
/![]() -plane) the system changes the discrete state, but does not modify the variables. Similar to the circle example, this illustrates the two sources of overapproximation: The overapproximation of the continuous trajectory in each quadrant, and the overapproximation resulting from the change of discrete state. In this example, the flowpipes hit the diagonal switching plane at an angle, such that many convex sets intersect with the plane and can take the transition. To reduce the number of sets, groups of them are clustered by taking their template hull. The preset clustering percentage for this example is 100, so all sets are clustered into a single convex set. Reduce the percentage to see more sets and flowpipes generated. In addition, try aggregating the clusters into a single convex set by changing the set-aggregation option to convex hull. This generates a single set, but being the convex hull of the clusters this can be significantly more precise than the template hull produced by clustering into a single set.
-plane) the system changes the discrete state, but does not modify the variables. Similar to the circle example, this illustrates the two sources of overapproximation: The overapproximation of the continuous trajectory in each quadrant, and the overapproximation resulting from the change of discrete state. In this example, the flowpipes hit the diagonal switching plane at an angle, such that many convex sets intersect with the plane and can take the transition. To reduce the number of sets, groups of them are clustered by taking their template hull. The preset clustering percentage for this example is 100, so all sets are clustered into a single convex set. Reduce the percentage to see more sets and flowpipes generated. In addition, try aggregating the clusters into a single convex set by changing the set-aggregation option to convex hull. This generates a single set, but being the convex hull of the clusters this can be significantly more precise than the template hull produced by clustering into a single set.
Reachability settings
We use as the initial set:
We consider a time horizon ![]() and the bad states are the states where
and the bad states are the states where ![]() .
.