Classification
| # of variables | # of modes | # of jumps |
|---|---|---|
| 2 | 1 | 1 |
| Type | Continuous dynamics | Guards & Invariants | Resets |
|---|---|---|---|
| hybrid | linear polynomial | half-space | linear |
Download
| Flow* | flow*_files |
| SpaceEx | spaceEx_files |
Model description
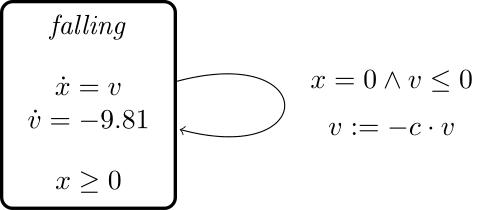
The classical bouncing ball example consists of a ball dropped from a predefined height. It hits the ground after a certain time, loses energy and then bounces back into the air and starts to fall again. This physical phenomena can be represented as the following hybrid automaton:
In the discrete state, the motion of the ball, assumed to have a mass of ![]() , is governed by the following differential equation:
, is governed by the following differential equation: ![]() where
where ![]() is the ball’s height from the ground,
is the ball’s height from the ground, ![]() is the ball’s vertical velocity, and
is the ball’s vertical velocity, and ![]() is the earth’s gravitational force. The invariant
is the earth’s gravitational force. The invariant ![]() enforces that the ball always bounces when it reaches the ground. The guard
enforces that the ball always bounces when it reaches the ground. The guard ![]() of the single discrete transition, which models the bouncing, ensures that bouncing happens after falling when reaching the ground. The corresponding reset condition
of the single discrete transition, which models the bouncing, ensures that bouncing happens after falling when reaching the ground. The corresponding reset condition ![]() accounts for the loss of energy due to the ball’s deformation, where
accounts for the loss of energy due to the ball’s deformation, where ![]() is a constant.
is a constant.
Reachability settings
We consider the inital set
![Rendered by QuickLaTeX.com x \in [10;10.2]](https://ths.rwth-aachen.de/wp-content/ql-cache/quicklatex.com-4bb483f219a05482e7cb7264c33e1067_l3.png)
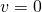 .
.
We use a time horizon of ![]() and set the constant
and set the constant ![]() . The set of bad states is the set of all states where
. The set of bad states is the set of all states where ![]() .
.
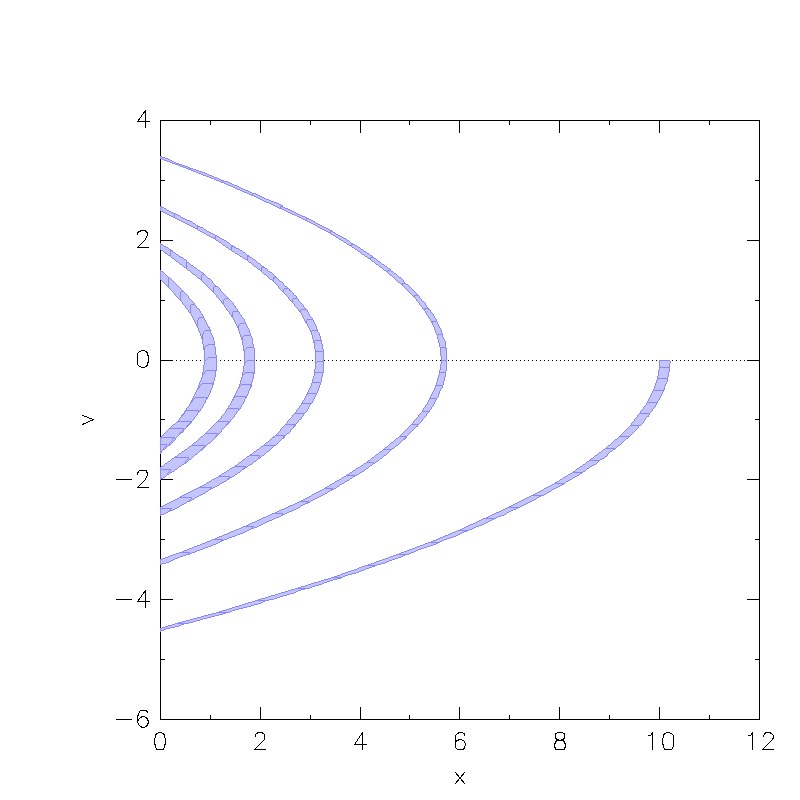
Results
These are the results from the bouncing ball benchmark created with SpaceEx: