Non-linear transmission line circuits | Theory of Hybrid Systems

Classification

# of variables	# of modes	# of jumps
n	3	2

Type	Continuous dynamics	Guards & Invariants	Resets
hybrid	non-polynomial	linear polynomial	identity

Note: The class of the benchmarks is determined by the input $i(t)$ .

Download

Flow* n=2	line_circuit_2.model
Flow* n=2	line_circuit_4.model
Flow* n=2	line_circuit_6.model
Flow* n=2	line_circuit_8.model
Flow* n=2	line_circuit_10.model
Flow* n=2	line_circuit_12.model

Model description

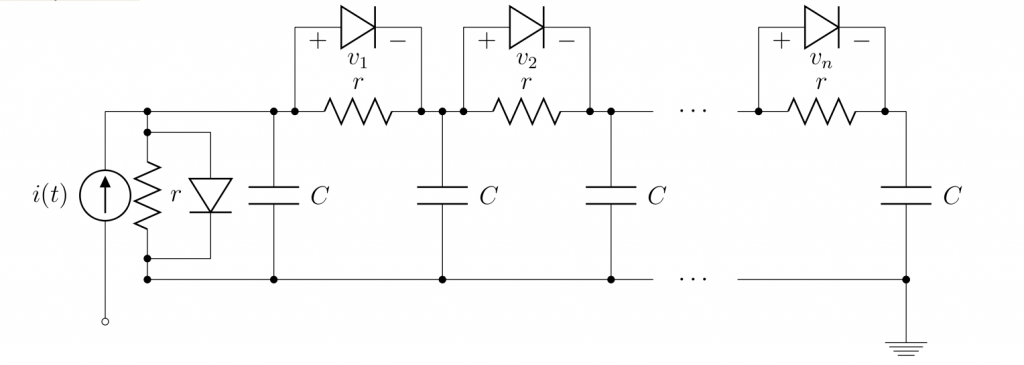
We study a non-linear resistor circuit which is shown in the figure below.

The circuit is composed of $n+1$ non-linear resistors and the same number of capacitors. Each non-linear resistor consists of a diode and a unit resistor ( $r = 1$ ). For simplicity, we assume that all capacitors have unit capacitance $C = 1$ . For each diode, the I-V characteristic is given by $I = \exp(K\cdot V) - 1$ . The value of $K$ is $40$ in the original model, but we set it as $5$ to relieve the stiffness of the behavior. The current source $i(t)$ in the figure is the input, and $v_1$ is the single output of the circuit. Therefore, the whole circuit system can be described by the following ODE.

$\left\{ \begin{array}{lcl} \dot{v}_1 & = & -2\cdot v_1 + v_2 + 2 - \exp(5\cdot v_1) - \exp(5\cdot (v_1 - v_2)) + i(t) \\ \dot{v}_2 & = & -2\cdot v_2 + v_1 + v_3 + \exp(5\cdot (v_1 - v_2)) - \exp(5\cdot (v_2 - v_3)) \\ & \cdots & \\ \dot{v}_{n-1} & = & -2\cdot v_{n-1} + v_{n-2} + v_n + \exp(5\cdot (v_{n-2} - v_{n-1})) - \exp(5\cdot (v_{n-1} - v_n)) \\ \dot{v}_n & = & -v_n + v_{n-1} - 1 + \exp(5\cdot (v_{n-1} - v_n)) \end{array} \right.$

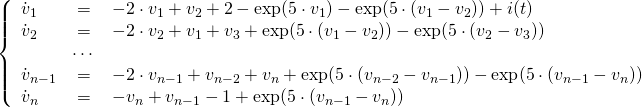
Scalable continuous and hybrid benchmarks can be built based on the circuit according to the size $n$ and various types of the input. Here, we consider a discontinuous input $i(t)$ which is defined by

$i(t) = \left\{ \begin{array}{ll} 2, & t\leq 1 \\ 3 - t, & 1 < t \leq 2 \\ 1, & t > 2 \end{array} \right.$

Reachability settings

The initial set under consideration is defined by $v_i \in [0,0.02]$ for $i=1,\dots,n$ .

Results

The following figure shows an overapproximation of the reachable set for the case $n=6$ over the time horizon $[0,3]$ computed by Flow*:

References

[1] M. Rewienski, J. White. A trajectory piecewise-linear approach to model order reduction and fast simulation of nonlinear circuits and micromachined devices. In IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, Volume 22(2), pages 155–170, IEEE, 2003.