Biological model I

Download

Flow* biology_I.model

Model description

We present a seven-dimensional continuous model which is adapted from a biological system given in [1]. The modeling ODE is given as below.

    \[ \left\{ \begin{array}{lcl} \dot{x}_1 & = & -0.4\cdot x_1 + 5\cdot x_3 \cdot x_4 \\ \dot{x}_2 & = & 0.4\cdot x_1 - x_2 \\ \dot{x}_3 & = & x2 - 5\cdot x_3 \cdot x_4 \\ \dot{x}_4 & = & 5\cdot x_5 \cdot x_6 - 5\cdot x_3 \cdot x_4 \\ \dot{x}_5 & = & -5\cdot x_5\cdot x_6 + 5\cdot x_3 \cdot x_4 \\ \dot{x}_6 & = & 0.5\cdot x_7 - 5\cdot x_5\cdot x_6 \\ \dot{x}_7 & = & -0.5\cdot x_7 + 5\cdot x_5\cdot x_6 \end{array} \right. \]

Reachability settings

We consider the initial set x_1,x_2,x_3,x_4,x_5,x_6,x_7\in [0.99,1.01] .

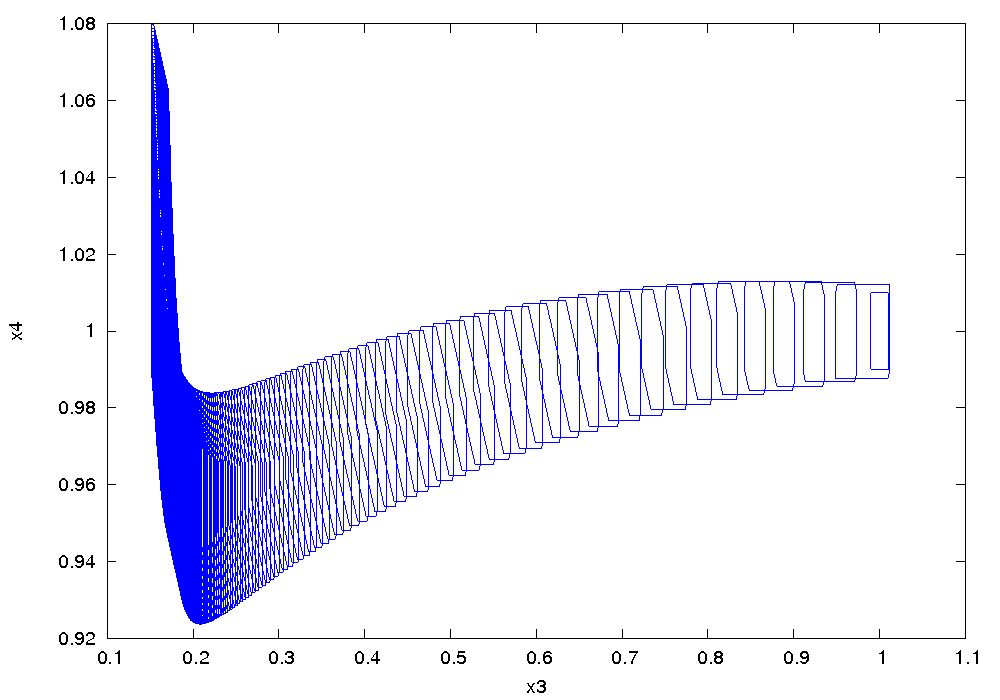
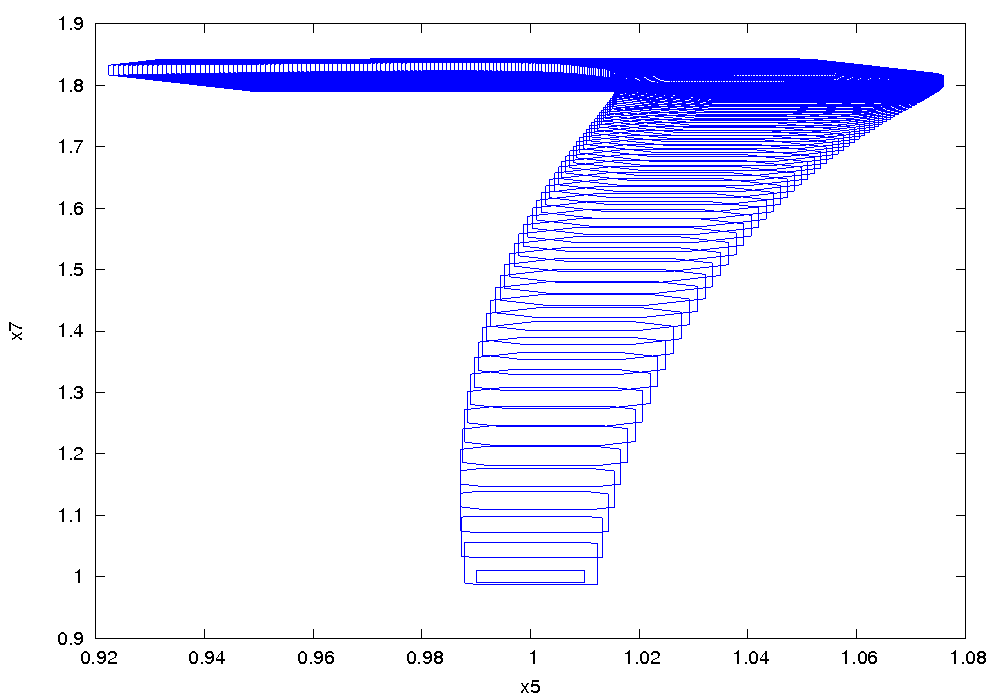
Results

The following figure shows an overapproximation computed by Flow* for the time horizon [0,2] :

biology_I_x3_x4

biology_I_x5_x7

References

[1] E. Klipp, R. Herwig, A. Kowald, C. Wierling, H. Lehrach. Systems Biology in Practice: Concepts, Implementation and Application. Wiley-Blackwell, 2005.